 dans lui-même, et on se limitera dans cette première approche à une fonction
dans lui-même, et on se limitera dans cette première approche à une fonction  .
.
CHAPITRE 2 :NOTION DE CHAOS
FICHIER MAPLE CORRESPONDANT : CHAOS.MWS
A ] Tentative de définition
Il n'existe pas encore de définition du chaos valable pour un système dynamique quelconque.
Néanmoins, la communauté scientifique s'accorde, dans le cas d'un système dynamique discret correspondant à une fonction d'un espace métrique dans lui-même, à le considérer comme chaotique s'il vérifie les propriétés suivantes:
1) La propriété de sensibilité.
2) La propriété de mélange.
3) La densité des points périodiques.
Dans la suite, on va s'attacher à définir plus précisément ces trois propriétés dans le cadre particulier d'une fonction d'un segment de  dans lui-même, et on se limitera dans cette première approche à une fonction
dans lui-même, et on se limitera dans cette première approche à une fonction  .
.
Ces définitions seront illustrées par l'exemple du système dynamique 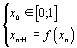 , avec
, avec  , dont on montrera grâce à de petits programmes MAPLE qu'il vérifie bien les propriétés d'un système chaotique.
, dont on montrera grâce à de petits programmes MAPLE qu'il vérifie bien les propriétés d'un système chaotique.
1) La sensibilité aux conditions initiales
Tout système dynamique, qu'il soit discret ou continu, est sensible aux conditions initiales, sauf s'il est totalement trivial. Ceci signifie que si l'on change l'état de départ, on s'attend à ce que l'évolution générale du système soit également modifiée. Par exemple, si une pierre d'une certaine masse est projetée avec une certaine vitesse initiale d'un certain point, le changement de la masse, du point de départ ou de la vitesse initiale va provoquer un changement de trajectoire.
Néanmoins, dans bon nombre de systèmes dynamiques, une petite erreur sur les conditions initiales va conduire à une erreur contrôlable sur les états suivants du système. Par exemple, si 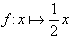 , et si
, et si 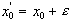 , alors
, alors  , ce qui fait que l'erreur relative
, ce qui fait que l'erreur relative  reste constante. Un tel système n'est pas chaotique, bien que sensible aux conditions initiales.
reste constante. Un tel système n'est pas chaotique, bien que sensible aux conditions initiales.
Pour le météorologue Lorenz, la caractéristique d'un système chaotique est que quelque soit l'erreur initiale  , après un certain nombre d'itérations (si l'on considère les systèmes discrets) l'erreur sera du même ordre que le signal lui-même.
, après un certain nombre d'itérations (si l'on considère les systèmes discrets) l'erreur sera du même ordre que le signal lui-même.
Par exemple, on peut vérifier que  conduit à un système dynamique de ce type en utilisant la procédure MAPLE comparaison, qui construit la "courbe"
conduit à un système dynamique de ce type en utilisant la procédure MAPLE comparaison, qui construit la "courbe" 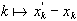 , le nombre d'itérations n, la valeur initiale x0 et l'erreur epsilon étant donnés. On remarque que quelque soit le choix de ces différents paramètres, on obtient au bout d'une vingtaine d'itérations une courbe qui a la même amplitude de valeurs (en fait
, le nombre d'itérations n, la valeur initiale x0 et l'erreur epsilon étant donnés. On remarque que quelque soit le choix de ces différents paramètres, on obtient au bout d'une vingtaine d'itérations une courbe qui a la même amplitude de valeurs (en fait  ) que celle de
) que celle de  (tester la procédure orbite avec le même n et le même x0). Ceci est typiquement le signe d'un comportement chaotique.
(tester la procédure orbite avec le même n et le même x0). Ceci est typiquement le signe d'un comportement chaotique.
Une définition plus précise de la sensibilité, appliquée au cas d'une fonction de  dans
dans  est la suivante:
est la suivante:
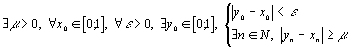
La borne supérieure de l'ensemble des  vérifiant cette condition est appelée la constante de sensibilité du système.
vérifiant cette condition est appelée la constante de sensibilité du système.
On peut remarquer que la définition ci-dessus est facilement généralisable si on remplace  par un segment quelconque (pas un intervalle quelconque, sinon on n'est pas assuré de l'existence de la constante de sensibilité).
par un segment quelconque (pas un intervalle quelconque, sinon on n'est pas assuré de l'existence de la constante de sensibilité).
De plus, elle est encore généralisable si l'on se place dans le cadre de certains espaces métriques plus généraux que 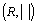 .
.
Remarque complémentaire:
Lors des premières itérations, la croissance de l'erreur est imperceptible sur les graphiques. Il est intéressant de savoir que pour ces premières itérations, à  fixé, et pour une petite erreur initiale
fixé, et pour une petite erreur initiale  , le système se comporte presque de façon linéaire, c'est à dire comme si la fonction était du type
, le système se comporte presque de façon linéaire, c'est à dire comme si la fonction était du type  , avec
, avec  .
.
Ceci est un comportement usuel dans ce type de système dynamique, et le nombre positif 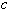 peut être déterminé expérimentalement de façon approchée, ou même parfois calculé avec des méthodes élémentaires de niveau Sup lorsque la fonction est suffisamment régulière. Pour certains systèmes dynamiques, il est intéressant à connaître (penser à l'exemple de la suivie d'une population d'animaux sur quelques générations).
peut être déterminé expérimentalement de façon approchée, ou même parfois calculé avec des méthodes élémentaires de niveau Sup lorsque la fonction est suffisamment régulière. Pour certains systèmes dynamiques, il est intéressant à connaître (penser à l'exemple de la suivie d'une population d'animaux sur quelques générations).
Le nombre  s'appelle l'exposant de Ljapounov de
s'appelle l'exposant de Ljapounov de  en
en  . Dans l'exemple
. Dans l'exemple  , vous pourrez vérifier empiriquement qu'il vaut
, vous pourrez vérifier empiriquement qu'il vaut  , indépendamment de
, indépendamment de  , c'est-à-dire que
, c'est-à-dire que 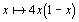 se comporte de façon analogue à
se comporte de façon analogue à  pour de petites valeurs de
pour de petites valeurs de  , pour ce qui concerne la croissance de l'erreur.
, pour ce qui concerne la croissance de l'erreur.
2) La capacité de mélange
Intuitivement, il s'agit de la propriété suivante: si l'on se donne deux sous-intervalles quelconques 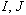 de
de  , le premier étant considéré comme source et le second comme cible, il existe une orbite dont le premier terme
, le premier étant considéré comme source et le second comme cible, il existe une orbite dont le premier terme  est dans
est dans  , et qui a l'un de ses éléments
, et qui a l'un de ses éléments  dans
dans  . Le caractère arbitraire des intervalles source et cible implique alors qu'en fait il existe une infinité de telles orbites, et que pour chacune d'entre elles, il existe une infinité d'éléments appartenant à l'intervalle cible.
. Le caractère arbitraire des intervalles source et cible implique alors qu'en fait il existe une infinité de telles orbites, et que pour chacune d'entre elles, il existe une infinité d'éléments appartenant à l'intervalle cible.
Plus précisément, la définition de la capacité de mélange est la suivante:

La capacité de mélange est a priori difficile à visualiser de façon satisfaisante, puisqu'aucune méthode n'est donnée pour le choix de  et que le premier terme
et que le premier terme 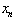 qui atteint l'intervalle cible peut être d'indice très élevé.
qui atteint l'intervalle cible peut être d'indice très élevé.
Pourtant, il se trouve que les systèmes chaotiques possèdent généralement une propriété voisine de la capacité de mélange, qui est celle de l'omniprésence des points à orbite ergodique. Une orbite est dite ergodique si l'ensemble de ses éléments est dense dans  , c'est-à-dire si tout sous-intervalle ouvert de
, c'est-à-dire si tout sous-intervalle ouvert de  contient un point de cette orbite. L'omniprésence signifie que si l'on prend un point "au hasard" dans
contient un point de cette orbite. L'omniprésence signifie que si l'on prend un point "au hasard" dans  , il est à orbite ergodique avec une probabilité égale à 1. Par exemple, on sait que l'ensemble des nombres rationnels et celui des irrationnels sont tous deux denses dans
, il est à orbite ergodique avec une probabilité égale à 1. Par exemple, on sait que l'ensemble des nombres rationnels et celui des irrationnels sont tous deux denses dans  , mais si l'on prend un nombre de
, mais si l'on prend un nombre de  au hasard, il a une probabilité nulle d'être rationnel, et égale à 1 d'être irrationnel (pour comprendre ce phénomène, imaginer que pour former un nombre de
au hasard, il a une probabilité nulle d'être rationnel, et égale à 1 d'être irrationnel (pour comprendre ce phénomène, imaginer que pour former un nombre de  , on tire au hasard la suite de ses chiffres dans son écriture décimale
, on tire au hasard la suite de ses chiffres dans son écriture décimale  . Former un nombre rationnel revient à tirer une suite de chiffres périodique à partir d'un certain rang, ce qui intuitivement - et on peut le montrer par un calcul élémentaire de probabilités - n'a aucune chance de se produire lorsque l'on fait une infinité de tirages).
. Former un nombre rationnel revient à tirer une suite de chiffres périodique à partir d'un certain rang, ce qui intuitivement - et on peut le montrer par un calcul élémentaire de probabilités - n'a aucune chance de se produire lorsque l'on fait une infinité de tirages).
Si un système possède cette propriété de l'omniprésence des points à orbite ergodique, il suffit de prendre un point au hasard dans l'intervalle source, et si l'on attend assez longtemps, l'un des itérés doit se retrouver dans l'intervalle cible. Ceci peut être effectivement testé pour  grâce à la procédure MAPLE mélange, dans laquelle l'on fournit le point initial x0, les bornes inférieure et supérieure gamma et delta de l'intervalle cible, et qui rend le couple (indice,valeur) correspondant au premier terme de l'orbite de x0 qui appartient à l'intervalle cible.
grâce à la procédure MAPLE mélange, dans laquelle l'on fournit le point initial x0, les bornes inférieure et supérieure gamma et delta de l'intervalle cible, et qui rend le couple (indice,valeur) correspondant au premier terme de l'orbite de x0 qui appartient à l'intervalle cible.
Cette propriété peut aussi être visualisée grâce à la procédure histogramme, qui prend en entrée un point initial x0, le nombre n d'itérations à effectuer, et le nombre précision qui définit le nombre de sous-intervalles d'égale longueur en lesquels on doit subdiviser  pour former le tableau des occurrences des éléments de l'orbite dans chacun de ces intervalles, et qui fournit en sortie l'histogramme des occurrences pour un point initial donné (on ne voit que les sommets des bâtons).
pour former le tableau des occurrences des éléments de l'orbite dans chacun de ces intervalles, et qui fournit en sortie l'histogramme des occurrences pour un point initial donné (on ne voit que les sommets des bâtons).
On peut remarquer que lorsqu'on augmente n, la courbe des sommets semble tendre vers une courbe régulière, symétrique par rapport à  , et qui représente à la limite la distribution des points de l'orbite dans
, et qui représente à la limite la distribution des points de l'orbite dans  .
.
Cette courbe, qui est donc la densité d'une probabilité, est en fait la courbe de  .
.
3) La densité des points périodiques
Cette propriété est simple à comprendre: dans tout sous-intervalle de  , il existe au moins un point périodique, c'est-à-dire dont l'orbite est un ensemble fini. On en déduit que tout sous-intervalle de
, il existe au moins un point périodique, c'est-à-dire dont l'orbite est un ensemble fini. On en déduit que tout sous-intervalle de  en contient alors une infinité.
en contient alors une infinité.
Par contre, cette propriété n'est pas visualisable, à cause de la propriété de sensibilité aux conditions initiales. En effet, un point périodique n'est en général pas codé dans la machine de façon exacte: il est arrondi, même si c'est à une très grande précision. Or cette erreur sur la valeur initiale - ou sur l'une des valeurs suivantes si par hasard la valeur initiale est codée de façon exacte - va faire évoluer le système de façon totalement différente, et même, on peut l'affirmer à coup sûr, selon une orbite ergodique...
On peut par exemple vérifier à la main que le point  est périodique de période 3, et cela apparaît au début du graphe obtenu par la procédure orbite, mais rapidement le comportement devient chaotique...
est périodique de période 3, et cela apparaît au début du graphe obtenu par la procédure orbite, mais rapidement le comportement devient chaotique...
A ce niveau, il est amusant de remarquer que si les points périodiques sont indécelables informatiquement dans un système chaotique, inversement toutes les orbites que l'on peut construire dans les procédures telles que orbite, comparaison, histogramme ou mélange sont en fait périodiques!
En effet, la machine ne peut coder de façon différente plus d'un nombre fini de nombres réels: par exemple, si elle travaille "à dix chiffres après la virgule", elle ne distingue dans  que
que  nombres différents. Au bout d'au plus
nombres différents. Au bout d'au plus  itérations de
itérations de  , elle va donc nécessairement calculer un terme déjà rencontré, et dès lors l'orbite deviendra cyclique. C'est le grand nombre d'itérations nécessaire en général pour que cela se produise qui fait que l'on ne s'en rend pas compte. On le verrait mieux si par exemple, on forçait tous les calculs à des résultats à deux chiffres après la virgule, avec la fonction MAPLE evalf(.,2).
, elle va donc nécessairement calculer un terme déjà rencontré, et dès lors l'orbite deviendra cyclique. C'est le grand nombre d'itérations nécessaire en général pour que cela se produise qui fait que l'on ne s'en rend pas compte. On le verrait mieux si par exemple, on forçait tous les calculs à des résultats à deux chiffres après la virgule, avec la fonction MAPLE evalf(.,2).
B ] Conclusion
Un dernier point, qui n'est pas totalement métaphysique, malgré les apparences, reste à élucider.
Est-il raisonnable de vouloir calculer des orbites pour un système chaotique, lorsqu'on sait que, d'une part les machines de calcul ne permettent pas de travailler avec une précision absolue, et que d'autres part la moindre erreur sur une valeur fait dévier complètement l'orbite, et ce de façon imprévisible?
La réponse est surprenante: il est vrai que toute orbite calculée est fondamentalement fausse, et ce - on l'a vu avec la procédure comparaison - au bout déjà d'une vingtaine d'itérations après la survenue d'une erreur, mais cependant quelque soit cette orbite fausse  , aussi petit soit le nombre
, aussi petit soit le nombre 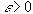 , il existe une orbite réelle
, il existe une orbite réelle  telle que
telle que  !
!
Ce résultat paradoxal s'appelle le lemme de l'ombre, parce que dans toute 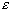 -ombre d'une orbite calculée, il existe une orbite bien réelle...
-ombre d'une orbite calculée, il existe une orbite bien réelle...
Donc, pour l'étude statistique d'un système chaotique, le lemme de l'ombre justifie les calculs informatiques que l'on peut faire. Il faut toutefois garder à l'esprit que pour 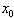 donné, le nombre que la machine donne pour
donné, le nombre que la machine donne pour  peut être n'importe quoi, et en tout cas est certainement sans rapport avec
peut être n'importe quoi, et en tout cas est certainement sans rapport avec  ...
...
La démonstration du comportement chaotique du système dynamique associé à 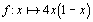 , selon les critères vus ci-dessus, ainsi que celle du lemme de l'ombre pour ce système, sera établie en résolvant le problème PBCHAOS.DOC (que malheureusement je n'ai pas :-( ).
, selon les critères vus ci-dessus, ainsi que celle du lemme de l'ombre pour ce système, sera établie en résolvant le problème PBCHAOS.DOC (que malheureusement je n'ai pas :-( ).